第10题
答案:
心得:
这道题目能够让你困惑的就是三角换元的回代问题了,sint,cost这些怎么求出来的?
瞧好了,小子,我只演示一遍
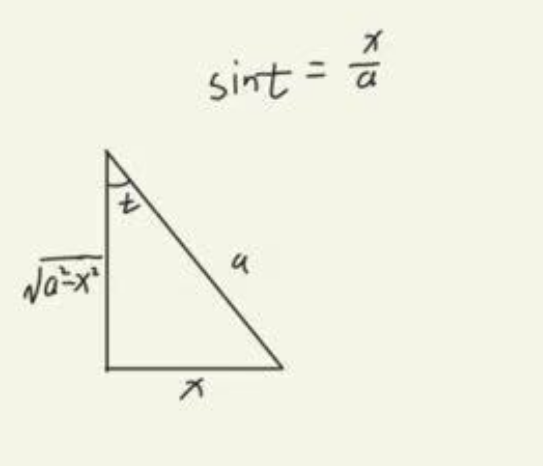
下面是我第二次做题的答案(错误的,用上我最喜欢绿色)
为什么错误?因为我太一味的追求想要的,忘记了这个过程是需要严谨的
我竟然试图从根式里面提出负号出来,是不是很傻瓜?如果你不觉得建议你也好好反省一下
正确答案所用公式,和错误答案所用公式如下
这道题,第一遍我甚至什么都看不出来,第二遍的时候想用第二类换元法(也就是三角换元,根式换元这些),因为我第二遍的时候刷了很多题目了
但是我又懒,于是仔细一瞄,那就凑微分呗,分子的x刚好,然后凑完了以后又懵了
因为这个时候还有一个分式和一个三角函数,我想把分式放后面,我竟然想的是ln求到为这个
傻瓜啊,那是分之一,这个是根号分之一,凑后面刚好是根号,还是题目写少了
以下是这个题目用到的公式
第一次写这道题的时候,我是直接从分母提出一个e的x次方,做出来和题目答案有差别,不知道是不是正确的
但是这种方法更简单,然后的话,这道题公式如下:
不瞒你说,第一次写这个题的时候,我就是这样写的,不同的是,我从分母提出e的x次方,答案都是这个
但是参考答案,是这样的
都怪我,太潦草了,囫囵吞枣,仔细一看
这题用的公式就不说了,都是简单的
碰到tan,就是想凑sec的平方来便于放到后面去
当然了,也不完全是,这道题,如果第一次没有经验,可能会将tan变为sin/cos,然后硬解
解的出来当然是 好事,但是当你耗费一大堆精力时间,发现结果错误,那g了
这道题所用公式:
难题,没得说,第二次还是做不出来,我第一眼看见会想分子是不是分母的求导结果,可是,不是
怎么办,想凑,死活不知道怎么凑,将分母展开更不行,那是打开潘多拉魔盒
算了,硬记这种方法吧,分子前面是1开头,我们可以同除x或者x方,将分母的x变1,那只能除x方
第二遍还是没有写出来,但是我隐约知道,要用下面的导数凑出一个式子,但是我只是将分母导数的系数定为1,造成
我即便是凑出来了,还是会出现约不掉的情况,原来是导数和后面约定为两个未知数
等我三刷吧
这道题第一遍刷的时候,头疼死我了,在脑海中始终有个声音告诉我说,什么和差公式,什么什么鬼的
想了无数时间,第二遍写的时候,觉得so easy,这个方法如果不做题真的想不出来,反正我不行
就是把分子化为分母的导数加上分母的倍数,这一题的方法和前面有一题是一样的
这道题目能够让你困惑的就是三角换元的回代问题了,sint,cost这些怎么求出来的?
瞧好了,小子,我只演示一遍
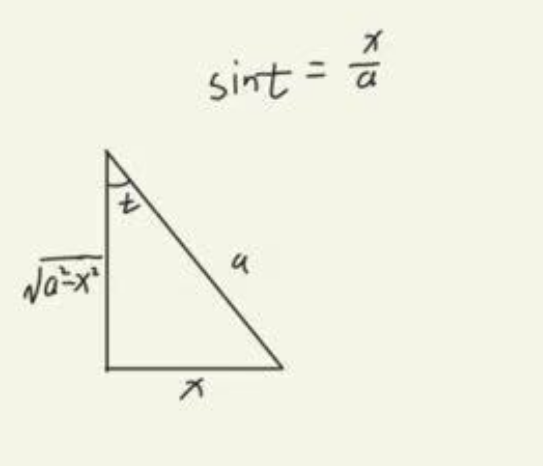
第二遍写的时候,一味的往下做,没有在关键的地方稍做停留,造成解答过程过于冗余复杂
以下是及时止损的答案
等着三刷吧你就,完全不在状态
我干,连续两天做不对,等着三刷吧你
这道题,以上是我第二遍第一次做错以后想了半天出来的,题目是运用有理分式分解直接分的,我是凑出来的
给你看看为什么我等于错在哪里
问题就出现在我把积分限外的符号放进来,直接套用那个积分公式,我到现在也没有搞懂为啥错了
于是只能将1-t的平方化为平方差公式拆分
当然你也可以试一试这个方法
这道题挺简单的,我做的时候犯了一个错误就是
我竟然系数写成1/2,因为我觉得要消掉2,所以我加个1/2,做题做糊涂了都
没啥好说的,我实力变牛逼了只能说😁😁😁
第一次我还傻乎乎的自以为是的化简,还换元,几步分部积分法就出来了
分部积分法就出来了,也不知道第一次写的时候犯什么病了
第二次还没有写出来,给了点提示以后竟然想凑平方,凑出来能干嘛?服了你了
答案也挺巧的,利用求出来的回看上一步才能消去,落子后还需重来才能看破迷局
第二遍,简单!
没什么好说的,简单
这道题二刷也没写出来,重点是我会就是分子为常数,分母是多项式,就是凑平方,但是上面含有x
不知道怎么办,原来是先看看分母的求导是什么,凑导数,消去x
不要怕用有理分式分解,我就是这样,老是觉得麻烦不敢用,一旦你无法了,记得分解不失为好方法
还是那句话,不要怕有理分式的分解!你越是嫌麻烦,越摸不透真相!
这道题我感觉确实挺那个啥的,真的,想三角换元不行,分部积分又不敢,我干,真的恶心
多少次了都不长记性,复合函数求导复合函数求导!!!!
卧槽,我真的变牛逼了嘿,当然了,还有标准答案也是,你只需要执行万能公式的转换就可以达到目标
第二遍还是没有写出来,原因在于太死板,三角换元有公式,但不一定必须使用公式规定的换元
其次正确换元以后,如何简单的化简不定积分是最重要的,说了,写一步考虑两步
不要当时爽了,事后就摆手了
涉及到三角换元,一定是要画图,进行回代的
愚蠢至极,不知道怎么想的,竟然想把x除下去凑1/x然后就解出来了,天下哪有这样的好事啊
老老实实写
我想到了用这种替换公式,但是我真的一直不敢下笔,觉得应该不是
并且我还发散去想万能公式,或者想一堆乱七八糟的,上下同除,或者什么的
麻辣,等着三刷
让你看看我的答案有多离谱,不知道为什么老是栽跟头在这里
看出来了吗?就是公式背错了我干
我第一遍的时候都能想到用三角代换,可是第二遍以后竟然越想越多反而造成不必要的麻烦
不知道怎么想的
唉,这道题还是稍微需要观察一下的,主要是分部积分以后分式的拆分有点难办
完全不上心啊,你就一步步来啊,试一试啊至少
没什么好说的,换元代入,求结果
按部就班,别把积分公式的几个根号,没有根号的记混了
这道题我知道了方法就是设x为tant,去掉反三角函数,但是在后面,一定不要忘记,当你看不出来的时候sin和cos才是最好的
这道题首先得会,万能公式,其次万能公式然后还要知道换元简化答案,不然你根本无从下手
三角万能公式是直接替换的
你每次都被牵着鼻子走,不该想的时候想到,该想的时候想不到
任何一个三角函数,都可以写成两个三角函数的导数和其本身的线性关系,当然我这里说的太过绝对,请自证
这一题辅助角公式秒了
看见三角函数的平方,可以优先考虑,sec函数因为平方可以凑后面变tan
看见三角函数的平方,可以优先考虑,sec函数因为平方可以凑后面变tan,而且很多时候,你是看不出来很多步的,你只能
走好目前的这一步,确保这一步是所有可能考虑到的情况中的最好的一步
不然你为什么看到答案会”啊,原来是这样“,你知道有这一步,但是你得考虑到啊
适当的将复杂的式子转化为t,变得好看些,反正也不影响结果嘛
没啥好说的,积化和差公式
头疼,三角函数这类题真的像找迷宫一样,找到一点算一点
这题有难度说实话,特别是还用到有理分式的拆分,巨巨巨巨恶心人,小心,当你代入t的值时,不要忘了等式右边的t也是具体值
能拆就拆
如果分子是乘积分母是加和,可以想平方公式