题目1
出错原因:
不会,第一步就开始找可疑点(无定义点),殊不知极限对n求,结果没有n,极限都没有求就开始找点了,你是真的牛逼
详细答案:

不会,第一步就开始找可疑点(无定义点),殊不知极限对n求,结果没有n,极限都没有求就开始找点了,你是真的牛逼

只会左右同时换个以e为底的步骤然后懵了,根号不知道怎么去
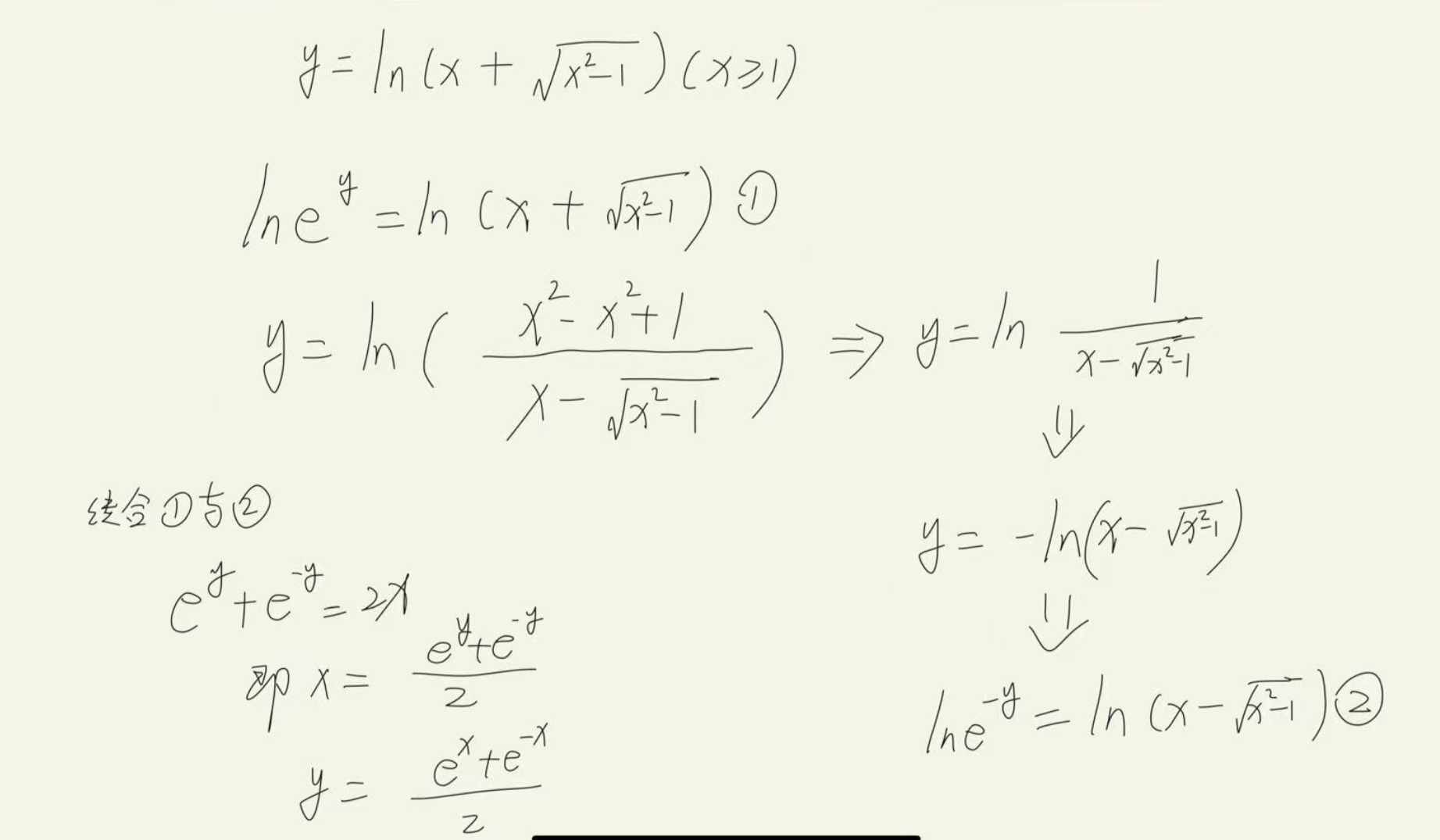
看到这道题第一步竟然不是想有理化,而是自以为是的提出根号x,还以为这样绝了
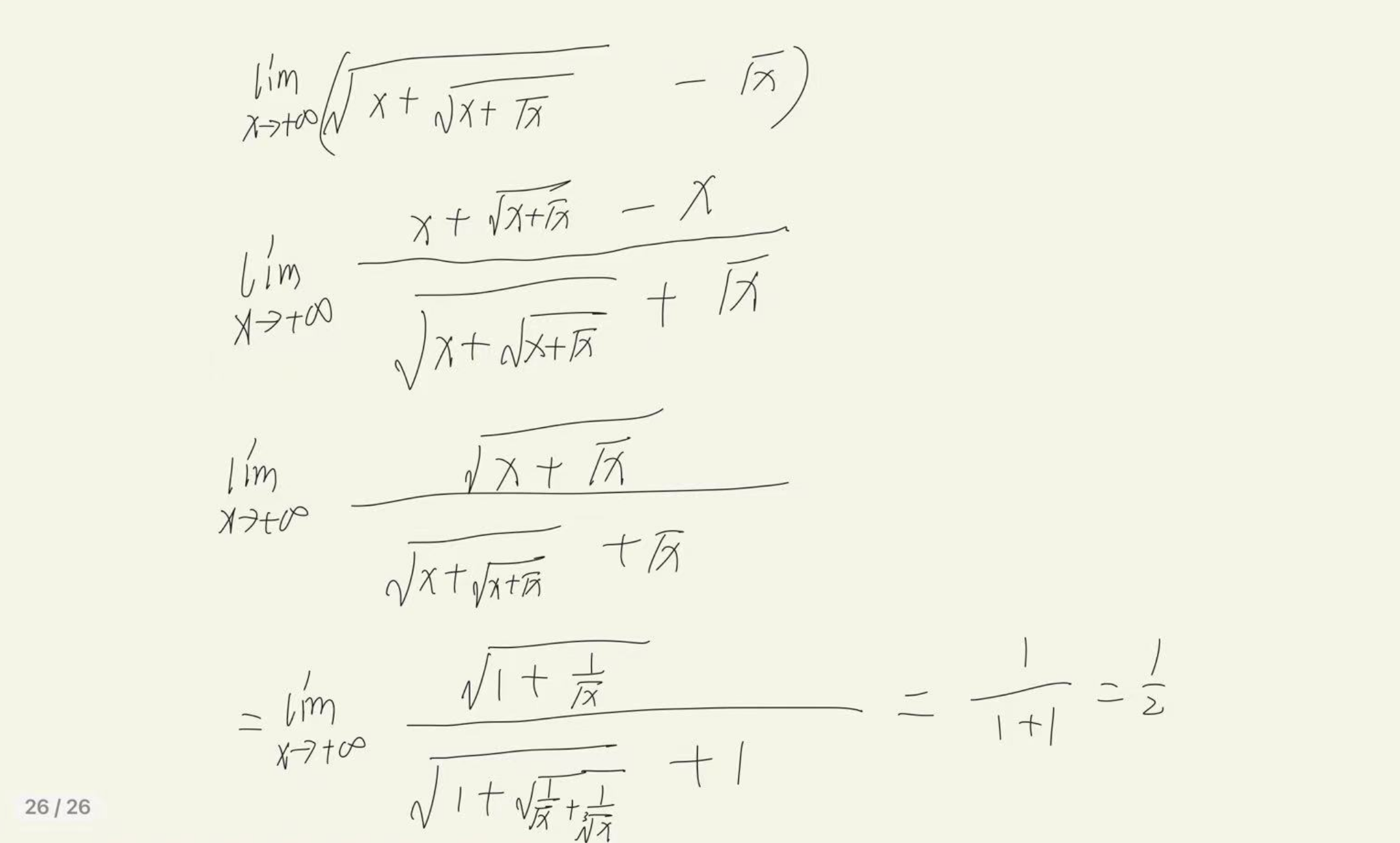
A.
B.
C.
D.
太久了,忘了
忘了
忘了
忘了
学了太多东西以后,竟然第一章的东西都快忘记的差不多了,间断点就只知道有两类了,都不知道求间断点的第一步是什么了
拿到题目完全没思路,完全不知道要干嘛,服了,就跟个傻蛋一样,就隐约感觉和拉格朗日中值定理有关系,但是人是开区间可导,闭区间连续,我去,不对,这不是柯西中值定理的条件吗,还有一大堆定理的条件,忘的差不多了,麻了
无
本来想先算一点找点规律的,但是直接cpu干冒烟了,你说气不气,完全超了我的思考范围,看了答案结果等比数列公式求和不会,直接爆炸
无
无
无
无
无
无
无
无
无
无
无
无
无
无
无
无
无
无
无
无